Introduction
In a nutshell, our research aims at developing theoretical understanding of, and experimental tools for, the magnetic confinement of a fusion plasma.
The thermonuclear fusion of deuterium and tritium, which are isotopes of hydrogen, at a temperature of 100 million degrees yields a huge amount of energy. At this temperature, matter takes the form of a plasma that tends to disperse and cool. In stars, gravity is enough to counteract this tendency: this is how stars produce their energy. A tokamak is a device that aims at reproducing this process, substituting gravity by the magnetic force. Magnetically controlled fusion is a good candidate to a new source of energy which would be renewable, abundant, clean, and economically viable. In the donut-shaped vessel of a tokamak, the plasma is confined by the superposition of two magnetic fields (toroidal and poloidal). It uses the properties of trajectories of charged particles in plasma that tend to curl around the field lines. The goal of a tokamak is to reach a quality of confinement such that fusion reactions are sufficient to maintain the required temperatures in the core of the plasma, and a radial gradient of temperature such that the edge of the plasma does not damage the wall of the vessel. However, particles suffer the effects of collisions and turbulence, resulting in a radial transport of heat at the expense of energy confinement. To combat this phenomenon, we must understand the mechanisms which are in the origin of radial transport: plasma instabilities. In an ignited tokamak, the confinement of high-energy particles that are born from fusion reactions is critical to prevent damages on the wall and to achieve a situation where the energy output is significantly larger than the input. A major concern is that these particles can excite plasma instabilities, so-called Alfvén Eigenmodes (AEs), which cause problematic radial transport. This issue has been recognized in the 1970's as one of the most challenging issues to be dealt with before achieving a viable fusion device. Since then, considerable progress has been made in the theoretical understanding of AEs. However, the estimation of their growth rate is complex, and the question of their stability in future burning plasma remains to be clarified. The analysis requires internal diagnostics that are not always available, and involves complicated mechanisms which details are still being debated. In general, these instabilities are described in a three-dimensional configuration space. However, if we assume that the modes are isolated, it is possible to use a mathematical transformation to reduce the problem to a set of one-dimensional equations, which have the same mathematical structure as the so-called Berk-Breizman (BB) model. The BB model is a generalization of the well-known equations that rule the evolution of an electrostatic wave that resonates with a beam of high-energy particles. In addition to these equations, the BB model includes a collision term that represents particle annihilation and injection processes, and an external wave damping accounting for background dissipative mechanisms.
Research topics
Our research activities were focused on the nonlinear trapping of particles in phase-space. Using our COBBLES code, we study:
- ion-acoustic turbulence;
- nonlinear bifurcations;
- nonlinear features of frequency sweeping (chirping). Chirping is a special kind of chaotic behavior where the mode frequency sweeps for a life-time of the order of a collision time. In general, two branches sweeping upwardly and downwardly coexist, and correspond to the evolution in phase-space of holes and clumps;
- subcritical instabilities, which are unstable solutions in a regime where linear theory predicts stability;
- the quantitative application of the BB model to AE experiments.
- the interactions between multiple resonances and the resulting phase-space turbulence.
- multiple holes/clumps interactions.
Numerical codes
We developed the numerical code COBBLES, which stands for COnservative Berk-Breizman semi-Lagrangian Extended Solver. COBBLES is capable of rigorous long-time computations of the BB model for experimentally relevant conditions, namely plasma where a beam of energetic particles is warm and much less dense than a cold, Maxwellian bulk. Rigorous simulation of these conditions is a challenging task since a weak, warm beam produces weak instabilities and small phase-space structures that are sensible to numerical errors such as numerical diffusion. We overcame these difficulties by implementing a numerical scheme that exactly conserves a flux balance of density between neighboring cells.
In addition, we developed a set of numerical tools for solving the linearized model equations, and for the analysis of nonlinear features of numerical and experimental data.
Validation of Berk-Breizman theory
For a cold bulk, weak warm beam, one dimensional plasma, we categorized the nonlinear evolution in the whole parameter space as damped, steady-state, periodic, chaotic or chirping. The saturation level of steady-state solutions, and the bifurcation between steady-state and periodic solutions near marginal stability match analytic predictions. The limit of a perturbative numerical approach when the resonant region extends into the bulk is shown. Frequency sweeping is observed, with time-evolution approaching theoretical results. A new method to extract the dissipation rate from frequency diagnostics is proposed.
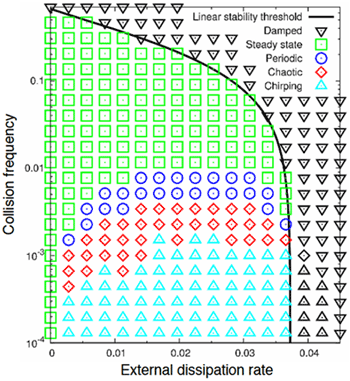 |
| Behavior bifurcation diagram for a cold bulk, weak warm beam distribution. The rates are normalized to the plasma frequency. The solid curve is the linear stability threshold obtained by solving the linear dispersion relation numerically. Diamonds and triangles on the right of the linear stability threshold, which are not included in the legend, represent sub-critical instabilities. |
Subcritical instabilities
We confirmed, for the first-time without assuming an adiabatic evolution of background particles, the existence of unstable solutions in nonlinear regimes where linear theory predicts the damping of the mode (subcritical solutions). We proposed a mechanism to explain this apparent contradiction between linear theory and the behavior of subcritical solutions at small perturbation amplitudes. We showed that, when the linear damping rate is sufficiently weak, small phase-space structures that are neglected in the linear theory can make the sign of the growth rate change. We delimited kinetic parameter regimes of the supercritical and subcritical domains.
Application to the Toroidal Alfven Eigenmode (TAE)
We compared two variants of the BB model, one which takes into account the evolution of bulk particles, and a perturbative variant that assume the bulk particles to evolve adiabatically. We determined that the perturbative version of the model is the most experimentally-relevant, since the effect of background plasma on AEs is yet unknown in the experiment. Within this assumption, we showed that three quantifiable nonlinear chirping characteristics are dictated by three fundamental kinetic parameters of the model. Based on these new findings, we developed a method to estimate the linear drive, external damping rate and effective collision frequency by fitting these chirping characteristics between AE experiments and the BB model. We applied this procedure by analyzing special AEs that own their existence to the geometry of a tokamak, Toroidicity-induced Alfvén Eigenmodes (TAEs). The kinetic parameters of TAEs on the European tokamak MAST are consistent with a former analysis that was performed using internal diagnostics and a three-dimensional, computer time-consuming, kinetic code. This agreement constitutes a first validation of our chirping features-matching technique. We then applied this method to experimental data of the Japanese tokamak JT-60U, yielding the first theoretical estimation of the kinetic parameters of TAEs in this device. The results suggest that the mode is a marginally unstable TAE, whose existence was not proved yet.